

(a) Show that there are two adjacent vertices of the same color. x 1, x 2, x 3 are the x coordinates of the vertices of a triangle. Question: Let each of the vertices of a regular 9- gon be colored black or white. #d_(B-C) = sqrt((color(red)(8) - color(blue)(12))^2 + (color(red)(4) - color(blue)(12))^2)#īecause #d_(A-B) = d_(A-C) = 10# these points are the vertices of an isosceles triangle. Then, AQ 2PD due to isosceles triangle PDQ and DT 1 2 PD due to 30-60. In an isosceles triangle, any 2 of the 3 sides are equal. #d_(A-C) = sqrt((color(red)(8) - color(blue)(18))^2 + (color(red)(4) - color(blue)(4))^2)# Ex 7.1, 4 Check whether (5, 2), (6, 4) and (7, 2) are the vertices of an isosceles triangle. Given points are the vertices of an isosceles triangle if measure of any two sides are equal. A triangle has three sides, three angles, and three vertices. #d_(A-B) = sqrt((color(red)(12) - color(blue)(18))^2 + (color(red)(12) - color(blue)(4))^2)# There are six types of triangles in total Isosceles, Scalene, Equilaterial, Oblique.
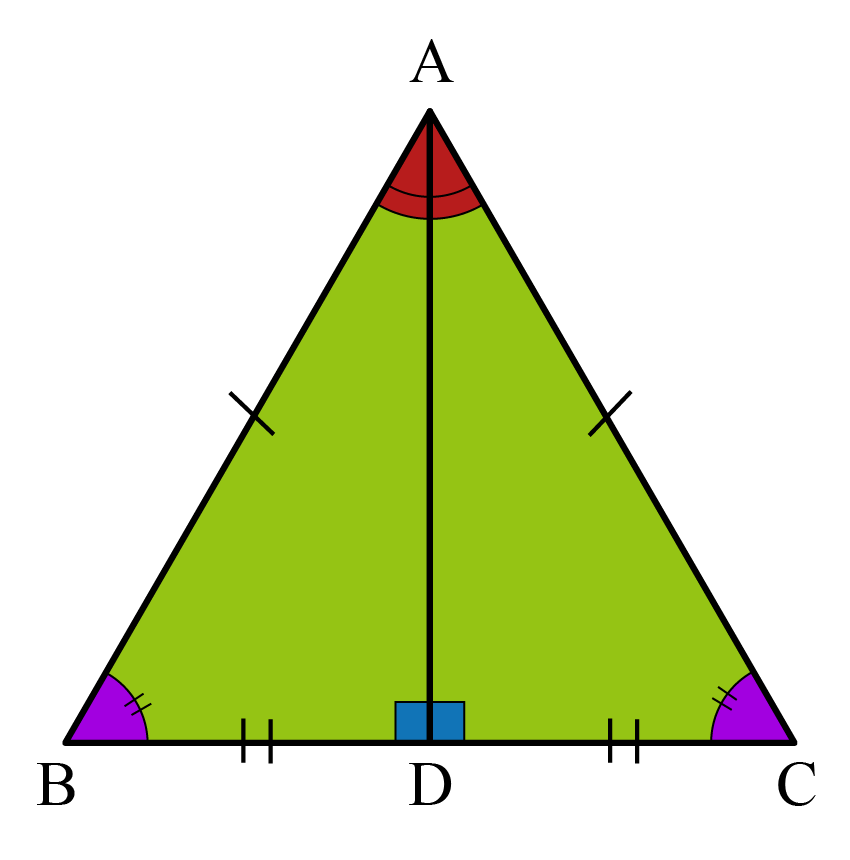
The formula for calculating the distance between two points is: If the triangle has two sides that have the congruent mark on them, you know that its isosceles. An obtuse angle measures more than 90 degrees, while an acute angle measures less than 90 degrees. If two are the same length then the points are the vertices of an isosceles triangle. No, the vertex angle of an isosceles triangle can be obtuse, acute, or a right angle. We can find the length of the three line segments.
An isosceles triangle has two sides the same length.


 0 kommentar(er)
0 kommentar(er)
